Lattice

基础

偏序(Partial Order)

在数学中（特别是集合论和序理论），偏序关系（partial order relation）是一种二元关系，它满足自反性、反对称性和传递性三个基本性质。以下是其精确定义：

设 $S$ 是一个非空集合（集合中的元素可以是任意对象）。一个二元关系 $R$ 定义在 $S$ 上（即 $R \subseteq S \times S$），称为偏序关系，当且仅当它满足自反性(Reflexivity)，反对称性(Antisymmetry)和传递性(Transitivity)。一个集合 $S$ 与定义在集合上的偏序关系 $R$ 被称作偏序集(partially ordered set, 或 poset)，表示为 $(S, R)$，$S$的成员被成为偏序集的元素。

习惯上，在任意偏序集$(S, R)$，符号 $a \preceq b$被用来表示$(a, b) \in R$。偏序关系也通常用符号$\leq$表示，当$(a, b) \in \leq$时，记作$a \leq b$。

如果一个偏序集合$(S, \preceq)$上的元素 $a$ 和 $b$满足$a \preceq b$或$b \preceq a$，我们称它们是可比较的(comparable)。如果既不满足$a \preceq b$ 也不满足 $b \preceq a$，则$a$ 和 $b$ 是不可比较(incomparable)。

如果存在偏序集$(S, \preceq )$，并且$S$中的每个元素都是可比较的，则 $S$ 是全序集(totally ordered set)或线型序集(linearly ordered set)，$\preceq$ 是全序(total order)或线性序(linear order)。一个全序集有时也被称作 链(chain)。

如果偏序集$(S, \preceq)$ 的 $\preceq$ 是全序并且$S$的每个非空子集都至少含有一个元素，则 $(S, \preceq)$是良序集(well-ordered set)。

字典序(Lexicographic Order)

Lexicographic Order（字典序）是一种基于已有顺序为序列（如字符串、元组、列表或笛卡尔积）定义全序关系的方法。其名称来源于字典中单词的排列规则：先比较首字母，若相同则比较第二个字母，依此类推。

设两个序列 $A = (a_1, a_2, \dots, a_m)$ 和 $B = (b_1, b_2, \dots, b_n)$，且序列元素所属的集合 $S$ 上已定义全序关系 $\leq$（如字母顺序、数值大小）。字典序 $\leq_{\text{lex}}$ 定义为：

$$A \leq_{\text{lex}} B \iff \begin{cases} \exists \, k \leq \min(m, n) : \\ \quad \forall i < k, \, a_i = b_i \, \land \, a_k \leq b_k, \quad \text{（前 \(k-1\) 个元素相等，第 \(k\) 个元素决定顺序）} \\ \text{或} \\ m \leq n \, \land \, \forall i \leq m, \, a_i = b_i. \quad \text{（\(A\) 是 \(B\) 的前缀）} \end{cases}$$

1. 全序性（Total Order）：

   • 若底层元素集 $S$ 是全序集，则字典序也是全序（任意两个序列可比）。
   • 例如：字母集 $S = \{a, b, c, \dots, z\}$ 按字母表顺序是全序，因此单词序列按字典序全序排列。

2. 递归比较：

   • 从第一个元素开始逐位比较，直到找到差异或一个序列结束。
   • 示例：比较 (2, 3, 5) 和 (2, 3, 4, 9)：
     • 前两位相同 $(2=2, 3=3)$ → 比较第三位：$5 > 4$ → 故 (2, 3, 5) > (2, 3, 4, 9)。

3. 前缀规则：

   • 若一序列是另一序列的前缀，则前缀更小。
   • 示例："cat" < "catalog"（因 "cat" 是 "catalog" 的前缀）。

严格字典序（Strict Lexicographic Order） 定义严格版本 $<_{\text{lex}}$：

$$A <_{\text{lex}} B \iff A \leq_{\text{lex}} B \land A \neq B.$$

• 示例："apple" < "apply"（前四位相同 appl，第五位 e < y）。

底层为偏序的情况 若元素集 $S$ 仅有偏序（非全序），则字典序仅为偏序：

• 示例：设 $S = \{x, y\}$ 且 $x$ 与 $y$ 不可比（即既非 $x \leq y$ 也非 $y \leq x$），则：
  • 序列$(x, y)$和$(y, x)$在字典序下不可比（因首元素不可比）。

哈斯图 (Hasse Diagrams)

Hasse 图是用于可视化有限偏序集（Partially Ordered Set, Poset）的简约图示方法，它通过省略冗余边（可由传递性和自反性推导出的关系），仅保留覆盖关系（covering relations），从而清晰展现偏序结构。

---

核心思想与定义

1. 覆盖关系（Covering Relation）： 在偏序集 $(P, \leq)$ 中，元素 $b$ 覆盖元素 $a$（记作 $a \lessdot b$），当且仅当：

   • $a < b$（即 $a \leq b$ 且 $a \neq b$），
   • 不存在中间元素 $z$ 满足 $a < z < b$。 例如：在整除序中，$2$ 覆盖 $1$（因无整数 $z$ 满足 $1 < z < 2$），但 $4$ 不直接覆盖 $1$（因存在 $2$ 满足 $1 < 2 < 4$）。

2. Hasse 图的构建原则：

   • 顶点：每个元素表示为平面上的点。
   • 边：仅当 $b$ 覆盖 $a$ 时，从 $a$ 到 $b$ 画一条无向线段（约定俗成：若 $a < b$，则 $b$ 画在 $a$ 上方）。
   • 省略：
     • 自反性：不画 $a \leq a$ 的自环。
     • 传递性：若 $a \lessdot b$ 且 $b \lessdot c$，则不直接画 $a$ 到 $c$ 的边（由路径隐含）。

---

绘制步骤

1. 分层排列：

   • 将极小元（minimal elements，无更小元素）置于底层。
   • 若 $b$ 覆盖 $a$，则 $b$ 放置在 $a$ 正上方（或斜上方）。
   • 同一水平层的元素不可比（incomparable）。

2. 恢复完整偏序：

   • $a \leq b$ 当且仅当存在一条从 $a$ 到 $b$ 的向上路径（路径可能经过多条边）。

---

关键性质

• 简约性：边数 $\leq |P| - 1$（远少于完整偏序图的 $O(|P|^2)$ 条边）。
• 无环：不含回路（因偏序是反对称的）。
• 方向隐含：所有边隐含向上方向（无需箭头）。

经典示例

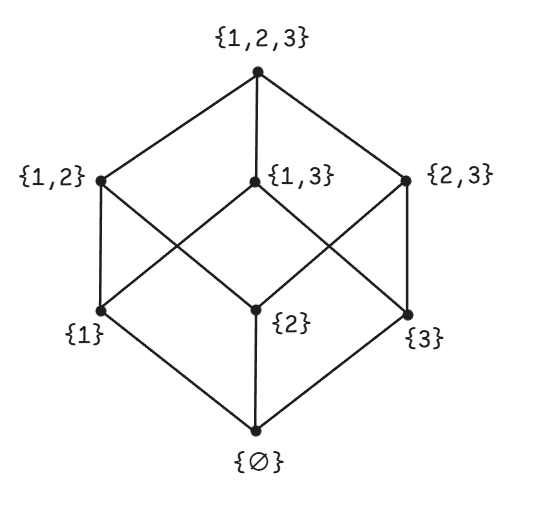
例1：集合 $S = \{1,2,3\}$ 的幂集（子集包含序 $\subseteq$）

• 元素：$\emptyset, \{1\}, \{2\}, \{3\}, \{1,2\}, \{1,3\}, \{2,3\}, \{1,2,3\}$
• 覆盖关系：
  • $\emptyset \lessdot \{1\}, \emptyset \lessdot \{2\}, \emptyset \lessdot \{3\}$
  • $\{1\} \lessdot \{1,2\}, \{1\} \lessdot \{1,3\}$
  • $\{2\} \lessdot \{1,2\}, \{2\} \lessdot \{2,3\}$
  • $\{3\} \lessdot \{1,3\}, \{3\} \lessdot \{2,3\}$
  • $\{1,2\} \lessdot \{1,2,3\}, \{1,3\} \lessdot \{1,2,3\}, \{2,3\} \lessdot \{1,2,3\}$
• Hasse 图：

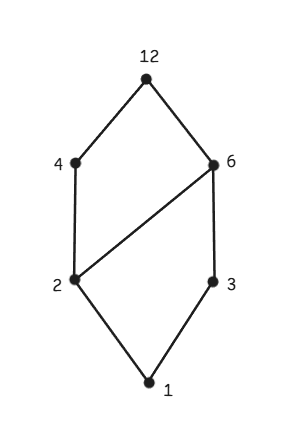
例2：整除序（$D_{12} = \{1,2,3,4,6,12\}$，关系为整除）

• 覆盖关系：
  • $1 \lessdot 2, 1 \lessdot 3$
  • $2 \lessdot 4, 2 \lessdot 6$
  • $3 \lessdot 6$
  • $4 \lessdot 12, 6 \lessdot 12$
• Hasse 图：

最大元素和最小元素(Maximal and Minimal Elements)

在偏序集$(S, \preceq)$中，如果不存在一个元素 $b$ 满足 $a \prec b$，则 $a$ 是最大的(Maximal)。同样的，如果不存在元素 $b$ 满足 $b \prec a$，则 $a$ 是最小的(Minimal)。

对于偏序集$(S, \preceq)$，对于所有$b \in S$，总满足 $b \preceq a$，则 $a$ 是偏序集中的最大元素(Greatest element)。如果最大元素存在，那么它是唯一的。同样，对于所有$b \in S$，总满足 $a \preceq b$，则 $a$ 是偏序集中的最小元素(Least element)。

在偏序集$(P, \preceq)$中，设$S \sube P$ 是任意子集：

---

1. 上界 (Upper Bound)

定义：元素 $u \in P$称为 $S$ 的上界，当且仅当：

$$\forall s \in S, \, s \preceq u$$

• 性质：
  • 上界可能不存在（如 (S) 无界）
  • 上界不一定唯一（可能有多个）
  • 上界不一定属于 (S)（通常 $u \notin S$）

---

2. 下界 (Lower Bound)

定义：元素 $l \in P$ 称为 $S$ 的下界，当且仅当：

$$\forall s \in S, \, l \preceq s$$

• 性质：
  • 下界可能不存在
  • 下界不一定唯一
  • 下界不一定属于 $S$

示例：

子集$\{a,b,c\}$的上界是 $e,f,j$ 和 $h$。它的下界只有 $a$。子集 $\{j,h\}$ 没有上界，它的下界是 $a, b, c, d, e$ 和 $f$ 。$a, c, d, f$ 的上界是 $f, h$ 和 $j$，它的下界是 $a$。

---

3. 最小上界 (Least Upper Bound, LUB) / 上确界 (Supremum)

定义：元素 $\sup S \in P$ 称为 $S$ 的最小上界，当且仅当：

$$\begin{aligned} &(1) \ \sup S \text{ 是 } S \text{ 的上界} \\ &(2) \ \forall u \in P, \, \text{若 } u \text{ 是 } S \text{ 的上界，则 } \sup S \preceq u \end{aligned}$$

• 性质：
  • 若存在则唯一（由反对称性保证）
  • 记作 $\sup S$ 或 $\bigvee S$
  • 不一定属于 $S$

示例：

• $S = (0, 1) \subseteq \mathbb{R}$: $\sup S = 1$ $(1 \notin S)$
• $S = \{ x \in \mathbb{Q} \mid x^2 < 2 \} \subseteq \mathbb{R}：$$\sup S = \sqrt{2}（$无理数）
• 不存在例：在 $\mathbb{Q}$中，$S = \{ x \in \mathbb{Q} \mid x^2 < 2 \}$无最小上界（因 $\sqrt{2} \notin \mathbb{Q}）$

---

4. 最大下界 (Greatest Lower Bound, GLB) / 下确界 (Infimum)

定义：元素 $\inf S \in P$ 称为 $S$ 的最大下界，当且仅当：

$$\begin{aligned} &(1) \ \inf S \text{ 是 } S \text{ 的下界} \\ &(2) \ \forall l \in P, \, \text{若 } l \text{ 是 } S \text{ 的下界，则 } l \preceq \inf S \end{aligned}$$

• 性质：
  • 若存在则唯一
  • 记作 $\inf S$或 $\bigwedge S$
  • 不一定属于 $S$

示例：

• $S = (0, 1) \subseteq \mathbb{R}$: $\inf S = 0$ $(0 \notin S)$
• $S = \{ \frac{1}{n} \mid n \in \mathbb{N} \} \subseteq \mathbb{R}$: $\inf S = 0（$$0 \notin S)$

---

存在性定理

1. 实数完备性公理： 在 $(\mathbb{R}, \leq)$中，任意有上界的非空子集必有最小上界（$\sup S$存在）。

2. 格 (Lattice)： 若偏序集 $(P, \leq)$中，任意两个元素 $\{a, b\}$都有最小上界 $\sup\{a,b\}$ 和最大下界 $\inf \{a,b\}$，则称为格。

   • 示例：
     • 幂集 $(\mathcal{P}(X), \subseteq)$：$\sup\{A,B\} = A \cup B$，$\inf\{A,B\} = A \cap B$
     • 正整数集 $(\mathbb{Z}^+, \mid)$ (整除序)：$\sup\{a,b\} = \text{lcm}(a,b)$，$\inf\{a,b\} = \gcd(a,b)$

拓扑排序(Topological Sorting)

拓扑排序是对有向无环图（DAG） 的顶点进行线性排序的算法，使得对于图中的每条有向边 $u \to v$，在排序中 $u$ 都出现在 $v$ 之前。它反映了顶点间的依赖关系，常用于任务调度、编译顺序等场景。

---

核心概念

1. 有向无环图（DAG）：

   • 有向边：表示顶点间的偏序关系（如任务依赖）
   • 无环：图中不存在循环依赖（否则拓扑排序不可能）

2. 偏序与全序：

   • 拓扑排序将偏序关系扩展为全序关系
   • 同一层级的顶点（无直接依赖）可任意排序

---

算法原理

拓扑排序的核心是逐步移除入度为0的顶点（无前置依赖的顶点），直到所有顶点被处理。

数学定义

设 DAG $G = (V, E)$：

• $V$：顶点集，$|V| = n$
• $E$：有向边集，$|E| = m$
• $\text{deg}^-(v)$：顶点 $v$ 的入度（指向 $v$ 的边数）

拓扑排序输出序列 $\sigma = [v_1, v_2, \dots, v_n]$ 满足：

$$\forall (u, v) \in E, \quad \sigma^{-1}(u) < \sigma^{-1}(v)$$

其中 $\sigma^{-1}(v)$ 表示 $v$ 在序列中的索引。

---

算法实现（Kahn 算法）

伪代码

function TopologicalSort(Graph G):
    1. 初始化:
        - 入度数组 indegree[1..n] ← 0
        - 队列 Q ← 空队列
        - 结果列表 L ← 空列表

    2. 计算入度:
        for each 边 (u, v) ∈ E:
            indegree[v] ← indegree[v] + 1

    3. 初始化队列:
        for each 顶点 v ∈ V:
            if indegree[v] == 0:
                Q.enqueue(v)

    4. 处理队列:
        while Q 非空:
            u ← Q.dequeue()
            L.append(u)  // 将 u 加入结果

            for each 邻接顶点 v of u:  // 遍历 u → v 的边
                indegree[v] ← indegree[v] - 1
                if indegree[v] == 0:
                    Q.enqueue(v)

    5. 检查环:
        if |L| < n:
            return "图中有环，拓扑排序不存在"
        else:
            return L

数学符号描述

$$\begin{aligned} &\text{输入: } G = (V, E) \\ &\text{输出: } \sigma = [v_1, v_2, \dots, v_n] \text{ 或错误} \\ \\ &\text{初始化:} \\ &\quad \forall v \in V, \text{deg}^-(v) \leftarrow \sum_{(u,v) \in E} 1 \\ &\quad Q \leftarrow \{ v \in V \mid \text{deg}^-(v) = 0 \} \\ &\quad L \leftarrow [] \\ \\ &\text{过程:} \\ &\quad \textbf{while } Q \neq \emptyset: \\ &\quad \quad u \leftarrow \text{dequeue}(Q) \\ &\quad \quad L.\text{append}(u) \\ &\quad \quad \textbf{for each } v \text{ such that } (u, v) \in E: \\ &\quad \quad \quad \text{deg}^-(v) \leftarrow \text{deg}^-(v) - 1 \\ &\quad \quad \quad \textbf{if } \text{deg}^-(v) = 0: \\ &\quad \quad \quad \quad \text{enqueue}(Q, v) \\ \\ &\quad \textbf{if } |L| < |V|: \\ &\quad \quad \textbf{return } \text{"Cycle Detected"} \\ &\quad \textbf{else:} \\ &\quad \quad \textbf{return } L \end{aligned}$$

算法特性

1. 时间复杂度：$O(|V| + |E|)$

   • 计算入度：$O(|E|)$
   • 每个顶点入队/出队一次：$O(|V|)$
   • 每条边处理一次：$O(|E|)$

2. 空间复杂度：$O(|V|)$

   • 存储入度数组和队列

3. 正确性保证：

   • 无环图：总能找到拓扑排序
   • 有环图：队列提前空，检测到环

示例演示

A → B → D
  ↘   ↗
    C

顶点入度：

• $\text{deg}^-(A) = 0$
• $\text{deg}^-(B) = 1$
• $\text{deg}^-(C) = 1$
• $\text{deg}^-(D) = 2$

执行过程：

1. 初始列队 $Q = \{ A \}$
2. 处理 $A$:
   1. $L= [ A ]$
   2. 更新 $B$ 入度 →0，$C$入度→0
   3. $Q = \{B, C\}$ （顺序任意）
3. 处理 $B$:
   1. $L = [A, B]$
   2. 更新 $D$ 入度→1
4. 处理 $C$:
   1. $L = [A, B, C]$
   2. 更新 $D$ 入度→0
   3. $Q = \{D\}$
5. 处理 $D$:
   1. $L = [A, B, C, D]$

合法拓扑序：$[A, B, C, D]$ 或 $[A, C, B, D]$。

格(Lattice)

格是一种具有特殊代数结构的偏序集，其中任意两个元素都有唯一的最小上界（join）和最大下界（meet）。

1. 核心定义

设 $(L, \leq)$ 是一个偏序集。若对任意两个元素 $a, b \in L$：

1. 最小上界（join） 存在：$\sup\{a, b\}$ 存在，记作 $a \vee b$
2. 最大下界（meet） 存在：$\inf\{a, b\}$ 存在，记作 $a \wedge b$

则称 $(L, \leq)$ 为一个格（Lattice）。当格满足以下条件时，称为 有界格：

• 存在 最小元 $\bot$ (bottom)：$\forall a \in L, \bot \leq a$
• 存在 最大元 $\top$ (top)：$\forall a \in L, a \leq \top$

在 有界分配格 中，若对元素 $a$ 存在元素 $b$ 满足：

1. $a \vee b = \top$
2. $a \wedge b = \bot$

则称 $b$ 是 $a$ 的 逆元 （或 补元），记为 $b = a'$ 或 $b = \neg a$

2. 等价代数定义

格也可定义为配备两个二元运算 $\vee$（并）和 $\wedge$（交）的集合 $L$，满足：

1. 交换律： $a \vee b = b \vee a$$a \wedge b = b \wedge a$
2. 结合律： $(a \vee b) \vee c = a \vee (b \vee c)$$(a \wedge b) \wedge c = a \wedge (b \wedge c$)
3. 吸收律： $a \vee (a \wedge b) = a$$a \wedge (a \vee b) = a$

偏序关系可通过运算恢复：

$$a \leq b \iff a \vee b = b \iff a \wedge b = a$$

关键特性

1. 有限子集的边界存在性： 在格中，任意有限非空子集都有最小上界和最大下界。

$$\sup\{a_1, \dots, a_n\} = a_1 \vee \cdots \vee a_n, \quad \inf\{a_1, \dots, a_n\} = a_1 \wedge \cdots \wedge a_n$$

2. 格同态（Lattice Homomorphism）：

   映射 $f: L_1 \to L_2$ 满足：

   $$f(a \vee b) = f(a) \vee f(b), \quad f(a \wedge b) = f(a) \wedge f(b)$$

3. 子格（Sublattice）：

   子集 $S \subseteq L$ 对 $\vee$ 和 $\wedge$ 运算封闭。

3. 格的分类

1. 有界格（Bounded Lattice）

   若存在元素 $\top$（最大元）和 $\bot$（最小元）满足：

   $$\forall a \in L, \quad a \leq \top, \quad \bot \leq a$$

   • 此时 $\bot \vee a = a$，$\top \wedge a = a$
   • 示例：幂集格 $(\mathcal{P}(X), \subseteq)$ 中，$\top = X$，$\bot = \emptyset$

2. 分配格（Distributive Lattice）

   满足分配律：

   $$a \vee (b \wedge c) = (a \vee b) \wedge (a \vee c), \quad a \wedge (b \vee c) = (a \wedge b) \vee (a \wedge c)$$

   • 非分配格示例：钻石格 $M_3$ 或五角格 $N_5$（下图）

         ⊤
        /|\
       a b c   --> 违反分配律：a ∧ (b ∨ c) = a ∧ ⊤ = a  
        \|/       但 (a ∧ b) ∨ (a ∧ c) = ⊥ ∨ ⊥ = ⊥
         ⊥

3. 模格（Modular Lattice）

   满足模律：

   $$\text{若 } a \leq b, \text{ 则 } a \vee (c \wedge b) = (a \vee c) \wedge b$$

   • 分配格一定是模格，反之不成立

4. 完备格（Complete Lattice）

   任意子集（包括无限子集）都有最小上界和最大下界。

   • Knaster-Tarski 定理：完备格上的单调函数有最小不动点

4. 示例

1. 子空间格

对于向量空间$V$的所有子空间构成的偏序集 $(\text{Sub}(V), \sube)$，任意两个子空间 $W_1$和$W_2$：

• 交(Meet)：

  $$W_1 \wedge W_2 = W_1 \cap W_2$$

  验证：

  1. 子空间封闭性：

     • 对任意 $u, v \in W_1 \cap W_2$ 和标量 $\alpha, \beta$：

       $$\alpha u + \beta v \in W_1 \quad \text{且} \quad \alpha u + \beta v \in W_2 \implies \alpha u + \beta v \in W_1 \cap W_2$$

     • 所以 $W_1 \cap W_2$ 是子空间

  2. 最大下界(GLB)：

     • 下界性：$W_1 \cap W_2 \sube W_1$ 且 $W_1 \cap W_2 \sube W_2$
     • 最大性：对任意子空间 $U$ 满足 $U \sube W_1$ 和 $U \sube W_2$，有 $U \sube W_1 \cap W_2$

• 和 (Join):

  $$W_1 \vee W_2 = W_1 + W_2 = \{ w_1 + w_2 | w_1 \in W_1, w_2 \in W_2 \}$$

  验证：

  1. 子空间封闭性：

     • 对任意 $u = u_1 + u_2$，$v = v_1 + v_2 \in W_1 + W_2$ 和标量 $\alpha, \beta$：

       $$\alpha u + \beta v = \underbrace{(\alpha u_1 + \beta v_1)}_{\in W_1} + \underbrace{(\alpha u_2 + \beta v_2)}_{\in W_2} \in W_1 + W_2$$

     • 所以 $W_1 + W_2$ 是子空间

  2. 最小上界(LUB)：

     • 上界性：$W_1 \sube W_1 + W_2$ (因 $w_1 = w_1 + 0$)，同理 $W_2 \sube W_1 + W_2$
     • 最小性：对任意子空间 $U$ 满足 $W_1 \sube U$ 和 $W_2 \sube U$，有 $w_1 + W_2 \in U$，故 $W_1 + W_2 \sube U$。

格的性质分析：

1. 有界格：

   • 最小元 $\bot = \{ 0 \}$ （零子空间）
   • 最大元 $\top = V$ （全空间）

2. 模格性(Modular Lattice)：

   子空间格满足模律：

   $$\text{若 } A \sube C \text{, 则 } A \vee (B \wedge C) = (A \vee B) \wedge C$$

   • 反例说明非分配性：

     取 $V = \mathbb{R}^2$，设：

     • $A = \text{span} \{(1, 0) \}$

     • $B = \text{span} \{(0, 1) \}$

     • $C = \text{span} \{(1, 1) \}$

       $$A \vee (B \wedge C) = A \vee \{ 0 \} = A, \quad (A \vee B) \wedge C = \mathbb{R}^2 \wedge C = C \neq A$$

       违反分配律，故为非分配格