SDN

路由选择算法

我们一般用图来形式化描述路由选择问题。我们知道图 $G = (N, E)$ 是一个 $N$ 个节点和 $E$ 条边的集合，其中每条边是取自 $N$ 的一对节点。

链路状态的路由选择算法 (LS 算法)

链路状态路由选择算法是一种分布式最短路径优先算法。其核心思想是：让网络中的每个路由器都掌握全网的完整拓扑结构，并各自独立地计算到达所有目的节点的最短路径。

在链路状态算法中，网络拓扑和所有的链路开销都是已知的，也就是说可用作 LS 算法的输入。实践中这是通过让每个节点向网络中所有其他节点广播链路状态分组来完成的，其中每个链路状态分组包含它所连接的链路的标识和开销。在实践中，这经常由链路状态广播(link state broadcast) 算法来完成。

Dijkstra算法

Dijkstra 算法计算从某节点（源节点）到网络中所有其他节点的最低开销路径。该算法是迭代算法，其性质是经过算法的第 $k$ 次迭代后，可知道到 $k$ 个目的节点的最低开销路径，在到所有目的节点的最低开销路径之中，这 $k$ 条路径具有 $k$ 个最低开销。我们定义下列记号。

• $D(v)$ : 到算法的本次迭代，从源节点到目的节点 $v$ 的最低开销路径的开销。
• $p(v)$ : 从源到 $v$ 沿着当前最低开销路径的前一节点 （ $v$ 的邻居）。
• $N'$ : 节点子集；如果从源到 $v$ 的最低开销路径已知，$v$ 在 $N'$ 中。

源节点 $u$ 的链路状态算法

Initialization:
N' = { u }
for all nodes v
	if v is a neighbor of u
		then D(v) = c(u, v)
	else
		D(v) = ∞
Loop
	find w not in N' such that D(w) is a minimum
	add w to N'
	update D(v) for each neighbor v of w and not in N':
		D(v) = min(D(v), D(w) + c(w, v))
	/* new cost to v is either old cose to v or known
		least path cost to w plus cost from w to v */
until N' = N

当LS算法终止时，对于每个节点，我们都得到从源节点沿着它的最低开销路径的前一节点。对于每个前一节点，我们又有它的前一节点，以此方式我们可以构建从源节点到所有目的节点的完整路径。通过对每个目的节点存放从 $u$ 到目的地的最低开销路径上的下一跳节点，在一个节点（如节点 $u$ ）中的转发表则能够根据此信息而构建。

拥塞敏感的路由选择振荡

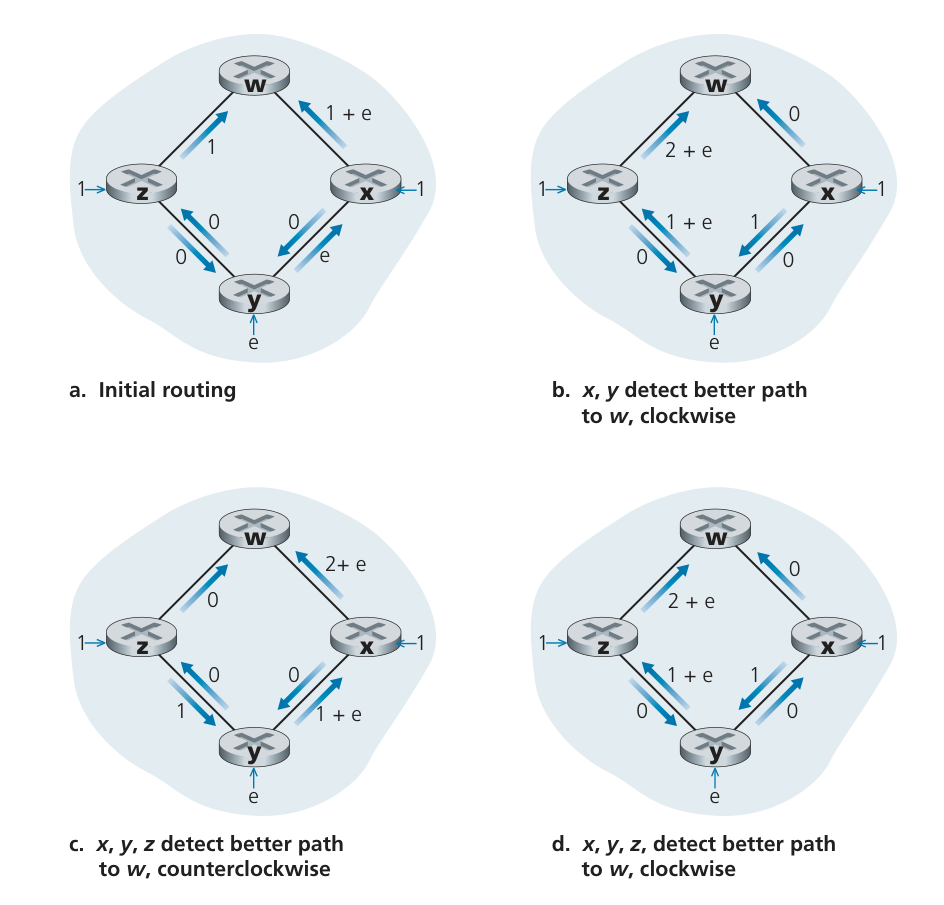
下图展示了一根简单的网络拓扑，图中的链路开销等于链路上承载的负载，例如反应要经历的时延。在该例中，链路开销是非对称的，即仅当在链路 $(u, v)$ 两个方向所承载的负载相同时 $c(u, v)$ 与 $c(v, u)$ 才相等。在该例中，节点 $z$ 产生发往 $w$ 的一根单元的流量，节点 $x$ 也产生发往 $w$ 的一个单元的流量，并且节点 $y$ 也产生发往$w$ 的一个数量为 $e$ 的流量。

当LS算法再次运行时，节点 $y$ 确定（基于图a所示的链路开销）顺时针到 $w$ 的路径为 1，而逆时针到 $w$ 的路径开销（一直使用的）是 $1 + e$。因此 $y$ 到 $w$ 的最低开销路径现在是顺时针的。类似的，$x$ 确定其到 $w$ 的新的最低开销路径也是顺时针的，产生如 图b 中所示的开销。当LS算法下次运行时，节点 $x, y$ 和 $z$ 都检测到一条至 $w$ 的逆时针方向的零开销路径，它们都将其流量引导到逆时针方向的路由上。下次LS算法运行时，$x, y$ 和 $z$ 都将其流量引导到顺时针方向的路由上。

距离向量路由选择算法 (DV 算法)

距离向量 算法是一种迭代的、异步的和分布式的算法。每个节点都要从一个或多个直接相连邻居接收某些信息，执行计算，然后将其计算结果分发给邻居。并且此过程一直要持续到邻居之间无更多信息要交换为止。此外，它不要求所有节点相互之间步伐一致地操作。

Bellman-Ford 方程

令 $d_x(y)$ 是从节点 $x$ 到节点 $y$ 的最低开销路径的开销。则该最低开销为

$$d_x(y) = min_v \{ c(x, v) + d_v(y) \}, \quad c(x,v) \text{表示 (x, v) 路径的开销}$$

方程中的 $min_v$ 是对于$x$的所有邻居的。Bellman-Ford 方程的解为节点 $x$ 的转发表提供了表项。令 $v^*$ 是取得方程中最小值的任何相邻节点。如果节点 $x$ 要沿着最低开销路径向节点 $y$ 发送一个分组，它应当首先向节点 $v^*$ 转发该分组。因此，节点 $x$ 的转发表将指定节点 $v^*$ 作为最终目的地 $y$ 的下一跳路由器。

算法描述

每个节点 $x$ 以 $D_x(y)$ 开始，对在 $N$ 中的所有节点 $y$，估计从 $x$ 到 $y$ 的最低开销路径的开销。令 $D_x = [D_x(y): y \in N]$ 是节点 $x$ 的距离向量，该向量是从 $x$ 到在 $N$ 中的所有其他节点 $y$ 的开销估计向量。使用 $DV$ 算法，每个节点 $x$ 维护下列路由选择信息：

• 对于每个邻居 $v$，从 $x$ 到直接相连邻居 $v$ 的开销为 $c(x, v)$。
• 节点 $x$ 的距离向量，即 $D_x = [D_x(y): y \in N]$，包含了 $x$ 到 $N$ 中所有目的地 $y$ 的开销估计值。
• 它的每个邻居的距离向量，即对 $x$ 的每个邻居 $v$ ，有 $D_v = [D_v[y) : y \in N]$。

在该分布式、异步算法中，每个节点不时地向它的每个邻居发送它的距离向量副本。当节点 $x$ 从它的任何一个邻居 $v$ 中接受到一个新距离向量，它保存 $v$ 的距离向量，然后使用 Bellman-Ford 方程更新它自己的距离向量如下：

$$D_x(y) = min_v \{ c(x, v) + D_v(y) \} \quad \text{对} N \text{中的每个节点}$$

如果节点 $x$ 的距离向量因这个更新步骤而改变，节点 $x$ 接下来将向它的每个邻居发送其更新后的距离向量，这继而让所有邻居更新它们自己的距离向量。只要所有节点继续以异步方式交换它们的距离向量，每个开销估计 $D_x(y)$ 收敛到 $d_x(y)$， $d_x(y)$ 为从节点 $x$ 到节点 $y$ 的实际最低开销路径的开销。

Initialization:
	for all destinations y in N
		D_x(y) = c(x, y)	/* if y is not a neighbor then c(x, y) = ∞ */ 
	for each neighbor w
		D_w(y) = ∞ for all destinations y in N
	for each neighbor w
		send distance vector D_x = {D_x(y) : y in N} to w
		
loop
	wait (until I see a link cost change to some neighbor w or
			until I receive a distance vector from some neighbor w)
			
	for each y in N:
		D_x(y) = min_v{ c(x, v) + D_v(y) }

if D_x(y) changed for any destination y
	send distance vector D_x = { D_x(y) : y in N } to all neighbors

forever

在该DV算法中，当节点 $x$ 发现它的直接相连的链路开销变化或从某个邻居接收到一个距离向量的更新时，它就更新新其距离向量估计值。但是为了一个给定的目的地 $y$ 而更新它的转发表，节点 $x$ 真正需要知道的不是到 $y$ 的最短路径距离，而是沿着最短路径到 $y$ 的下一跳路由器邻居节点 $v^*(y)$ 。下一跳路由器 $v^*(y)$ 是在 DV 算法中取得的最小值的邻居 $v$ 。

下图展示了 DV 算法的运行，应用场合是该图顶部有三个节点的简单网络。算法的运行以同步的方式显示出来，其中所有节点同时从其邻居接收报文，计算其新距离向量，如果距离向量发生了变化则通知其邻居。

该图最左边一列显示了这3个节点各自的初始路由选择表(routing table)。在一张特定的路由选择表中，每行是一个距离向量——特别是每个节点的路由选择表包括了它的距离向量和它的每个邻居的距离向量。因此，在节点 $x$ 的初始路由选择表中的第一行是 $D_x = [ D_x(x), D_x(y), D_x(z)] = [0, 2, 7]$ 。在该表的第二和第三行是最近分别从节点 $y$ 和 $z$ 收到的距离向量。因为在初始化时节点 $x$ 还没有从 $y$ 和 $z$ 收到任何东西，所以第二行和第三行表项中被初始化为无穷大。

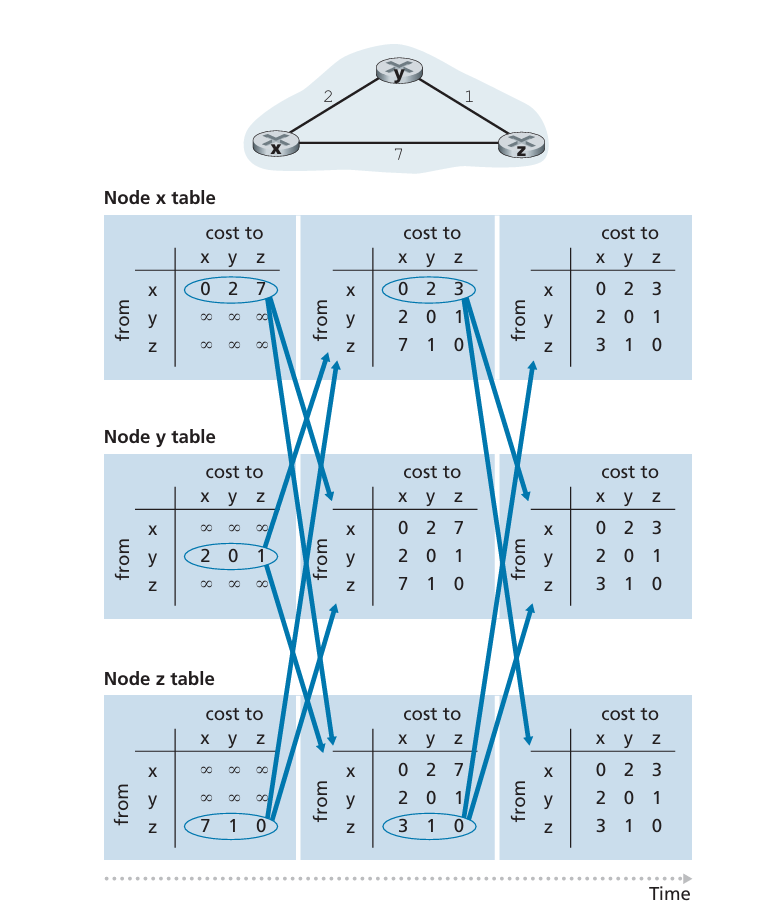
初始化后，每个节点向它的两个邻居发送其距离向量。在接收到该更新后，每个节点重新计算它自己的距离向量。例如，节点$x$向两个节点 $y$ 和 $z$ 发送了它的距离向量 $D_x = [0, 2, 7]$。在接收到该更新后，每个节点重新计算它自己的距离向量。例如，节点 $x$ 计算

\begin{flalign} D_x (x) &= 0 \\ D_x (y) &= min\{ c(x, y) + D_y(y), \, c(x, z) + D_z(y) \} = min \{ 2 + 0, \, 7 + 1 \} = 2 \\ D_z(z) &= min\{ c(x, y) + D_y(y), \, c(x, z) + D_z(z) \} = min \{ 2 + 1, 7 + 0 \} = 3 \end{flalign}

在节点重新计算它们的距离向量之后，它们再次向其邻居发送它们的更新距离向量（如果它们已经改变的话）。上图的第二列和第三列展示了这一过程。注意仅有节点 $x$ 和 节点 $z$ 发送了更新：节点 $y$ 的距离向量没有发生变化，因此节点 $y$ 没有发送更新。在接受到这些更新后，这些节点重新计算它们的距离向量并更新它们的路由选择表，这些显示在第三列中。

从邻居接收更新距离向量、重新计算路由选择表项和通知邻居到目的地的最低开销路径的开销已经变化的过程继续下去，直到无更新报文发送为止。在这个时候，因为无更新报文发送，将不会出现进一步的路由选择表计算，该算法将进人静止状态，即所有的节点将执行DV算法的第10~11行中的等待。该算法停留在静止状态，直到一条链路开销发生改变。

1. 距离向量算法：链路故障

现在考虑当某链路开销增加时发生的情况。假设 $x$ 与 $y$ 之间的链路开销从 $4$ 增加到 $60$，

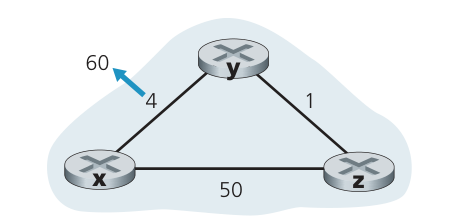
1. 在链路开销变化之前，$D_y(x) = 4, D_y(z) = 1, D_z(y) = 1$ 和 $D_z(x) = 5$。在 $t_0$ 时刻，$y$ 检测到链路开销变化（开销从 4 变为 60）。$y$ 计算它到 $x$ 的新的最低开销路径的开销，其值为

$$D_y(x) = min \{ c(y, x) + D_x(x), c(y, z) + D_z(x) \} = min \{ 60 + 0, 1 + 5 \} = 6$$

从网络全局的视角来看，我们能够看出经过 $z$ 的这个新开销时错误的。因为 $z$ 到 $x$ 的最低开销路径为 $ z \to y \to x$ ，但此时 $x$ 与 $y$ 之间的链路开销已经更改，而对于节点 $z$ 来说，此时它仍然不知道当前网络中某条链路开销已经发生变化，所以对于所有不直接与这条变化的链路相连的节点来说，它们都认为自己的距离向量值为正确的（实际上很可能是错误的）。而对于与这条链路相连的节点($x, y$)来说，它们在计算距离向量时使用了错误的值（这些值来自于其他的节点）。到了 $t_1$ 时刻，我们遇到路由选择环路(routing loop)，即为到达 $x$，$y$ 通过 $z$ 路由，$z$ 又通过 $y$ 路由。路由选择环路就像一个黑洞，即目的地为 $x$ 的分组在 $t_1$ 时刻到达 $y$ 和 $z$ 后，将在这两个节点之间不停地（或直到转发表发生改变为止）来回反复。

2. 因为节点 $y$ 已算出到 $x$ 的新的最低开销，它在 $t_1$ 时刻将该新距离向量通知 $z$。

3. 在 $t_1$ 后某个时间，$z$ 收到 $y$ 的新距离向量，它指示了 $y$ 到 $x$ 的最低开销是 $6$。$z$ 知道它能以开销 1 到达 $y$ ，因此计算出到 $x$ 的新最低开销 $D_z(x) = min \{ 50 + 0, 1 + 6 \} = 7$ 。因为 $z$ 到 $x$ 的最低开销已增加了，于是它便在 $t_2$ 时刻通知 $y$ 其新开销。

4. 以类似方式，在收到 $z$ 的新距离向量后，$y$ 决定 $D_y(x) = 8$ 并向 $z$ 发送其距离向量。接下来 $z$ 确定 $D_z(x) = 9$ 并向 $y$ 发送其距离向量，等等。

该循环将持续 44 次迭代（在 $y$ 与 $z$ 之间交换报文），即知道 $z$ 算出它经由 $y$ 的路径开销大于 50 (大于 $z \to x$ 这条链路的开销)为止。此时，$z$ 将（最终）确定它到 $x$ 的最低开销路径是经过它到 $x$ 的直接连接。$y$ 将经由 $z$ 路由选择到 $x$ 。

2. 距离向量算法：增加毒性逆转

刚才描述的特定循环的场景可以通过使用一种称为 毒性逆转 (poisoned reverse) 的技术而加以避免。其思想较为简单：如果 $z$ 通过 $y$ 路由选择到目的地 $x$，则 $z$ 将通告 $y$ ，它（即 $z$ ）到 $x$ 的距离是无穷大，也就是 $z$ 将向 $y$ 通告 $D_z(x) = \infty$ （即使 $z$ 实际上知道 $D_z(x) = 5$）。只要 $z$ 经过 $y$ 路由选择到 $x$ ，$z$ 就持续地向 $y$ 讲述这个善意的谎言。因为 $y$ 相信 $z$ 没有到 $x$ 的路径，故只要 $z$ 继续经 $y$ 路由选择到 $x$ （并这样撒谎），$y$ 将永远不会试图经由 $z$ 路由选择到 $x$ 。

毒性逆转并没有解决一般的无穷计数问题，当涉及到3个或更多节点（而不只是两个直接相连的邻居节点）的环路将无法用毒性逆转技术检测到。

基于流的转发

流表是SDN交换机的“心脏”，它取代了传统交换机中的MAC地址表和路由器中的路由表。

一张流表由多条 “流表项” 组成，每个流表项通常包含以下几个核心部分：

• 匹配域：定义了一组规则，用于识别特定的“流”。交换机将入站数据包的多个包头字段与这些规则进行匹配。
• 优先级：当一条数据包匹配上多条流表项时，优先级最高的项生效。
• 计数器：当数据包匹配成功时，更新计数器（如收发包数量、字节数）。
• 指令/动作：指定匹配成功的数据包应该执行什么操作。

匹配域极其灵活，它可以检查网络模型中第二层（数据链路层）、第三层（网络层）、第四层（传输层）甚至更高层的包头字段。比如二层的入端口、源MAC地址、目的MAC地址、以太网类型，三层的 源IP地址、目的IP地址、IP协议类型，四层的源TCP/UDP端口、目的TCP/UDP端口，或是其他字段VLAN ID、MPLS标签等。

一个流表项可以指定一个或多个动作。常见的动作包括：

• 转发：将数据包从指定的物理端口发送出去。
• 丢弃：直接丢弃数据包，不进行转发。
• 修改：修改数据包的包头字段，如修改源/目的MAC地址、IP地址、端口号。
• 发送到控制器：如果交换机不知道如何处理这个流，就将数据包封装在Packet-in消息中发送给控制器，由控制器决策。

数据平面与控制平面分离

数据平面由网络交换机组成，交换机是相对简单但快速的设备，该设备在它们的流表中执行“匹配加动作”的规则。控制平面由服务器以及决定和管理交换机流表的软件组成。

网络控制功能

与传统的路由器不同，在SDN中，控制软件运行在服务器上（而不是网络交换机），该服务器与网络交换机截然分开并与之远离。控制平面自身由两个组件组成：一个SDN控制器，以及若干网络控制应用程序。

可编程网络

通过运行在控制平面中的网络控制应用程序，该网络是可编程的。这些应用程序使用了由SDN控制器提供的API来定义和控制网络设备中的数据平面。例如，一个路由选择网络控制应用程序可以决定源和目的地之间的端到端路径（例如，通过使用由SDN控制器维护的节点状态和链路状态信息，执行Dijkstra算法）。另一个网络应用程序可以执行访问控制，即决定交换机阻挡哪个分组。还有一个应用程序可以用执行服务器负载均衡的方式转发分组。